CÁLCULO DEL ESQUELETO EN LA PROYECCIÓN DE MERCATOR

José Manuel Millán Gamboa, Instituto Hidrográfico de la Marina
Jefe Producción de Cartografía Electrónica (ENC), (2004) Instituto Hidrográfico de la Marina.

El problema del cálculo del esqueleto consiste en la determinación de las dimensiones de una carta Mercatoriana y la distribución de los paralelos y meridianos que forman el reticulado geográfico de esa carta. Para resolver este problema se emplearán las fórmulas de correspondencia estipuladas para este tipo de transformación. En la sección Algunas utilidades se incluye una hoja de cálculo Excel™ con la implementación de estas fórmulas.

Los datos de partida para su resolución son los marcos N y S de la carta, definidos por sus respectivas latitudes, los marcos E y W, definidos por sus respectivas longitudes, la latitud del paralelo de referencia, la escala, el intervalo entre meridianos, y el intervalo entre paralelos, normalmente dado en minutos. Las incógnitas son las dimensiones vertical y horizontal de la carta, las distancias desde el marco S a cada paralelo, y las distancias desde el marco W a cada meridiano.

El marco SW será el que se tome como origen de coordenadas para definir las distancias x a cada meridiano, y las distancias y a cada paralelo. Este origen de coordenadas, será sobre el que se den los resultados, pero para llegar a ello, antes se utilizará el sistema de coordenadas rectangulares, más general, cuyo origen coincidirá con aquel punto del Ecuador que se encuentra en el meridiano de Greenwich, es decir, el punto de latitud 0º, y longitud 0º. Para conformar el reticulado geográfico se emplearán unidades exactas de grados, minutos o segundos, excepto en el caso de los marcos que serán elegidos según criterios cartográficos. Las fórmulas de correspondencia permiten calcular las coordenadas (x, y) de un punto P’ sobre el plano de representación, correspondiente a un punto P(f, l) sobre el elipsoide:

Para más información véase el artículo sobre el cálculo de coordenadas en la proyección Mercator

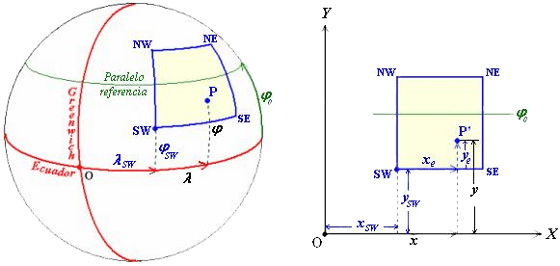
Como en esas fórmulas el valor del semieje mayor a se introduce en metros, resultará que las coordenadas (x, y) obtenidas, también vendrán dadas en metros, y medidas desde el origen de coordenadas O’ (x = 0, y = 0) del plano, que se corresponde con el punto O de coordenadas (f=0, l=0) sobre el elipsoide. Para calcular los elementos del esqueleto, se tomará como nuevo origen de coordenadas su esquina SW, es decir el punto de coordenadas (x_SW, y_SW) sobre el plano, o su correspondiente (f_SW, l_SW) sobre el elipsoide. Tal como se muestra en la figura anterior, para convertir las coordenadas de cualquier punto x, y a coordenadas esqueleto x_e, y_e con origen en las esquina SW del marco, se deberán calcular las diferencias:

Los valores x_e e y_e, así calculados, vendrán dados en metros medidos sobre el terreno, ya que no se ha tenido en cuenta ninguna escala de representación para la futura carta hasta el momento. Así, para una escala de representación E = 1:M, habrá que multiplicar todos los valores a por E. Además, los resultados de cualquier pareja de coordenadas (x_e, y_e), para confeccionar la carta, suelen darse en milímetros respecto al origen SW, por lo que también habrá que multiplicar por el factor 10³. Teniendo en cuenta estas consideraciones, se pueden dar unas expresiones que dan las coordenadas x_e e y_e de cualquier punto del esqueleto, respecto a su origen SW, con escala y en milímetros:

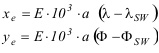
Ahora bien, hasta ahora se ha considerado como cilindro de proyección, aquel que es tangente al elipsoide a lo largo del Ecuador. Pero si se utiliza el artificio del paralelo de referencia en una latitud f₀, se producirá una reducción de escala respecto del modelo original con el cilindro tangente en el Ecuador. Dicha reducción, viene dada por la relación:

Por tanto, las coordenadas x_e e y_e, de cualquier punto del esqueleto respecto a su origen SW, con escala, en milímetros, referidos a un paralelo de referencia f₀, e introduciendo latitudes y longitudes en minutos, vendrán dadas por:

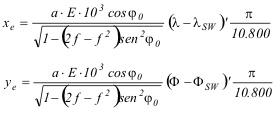
En estas fórmulas interviene el siguiente factor, que se denominará i_u, y que corresponde a la longitud de 1 minuto de paralelo de referencia f₀, con escala y en milímetros:

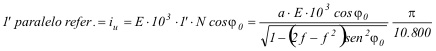
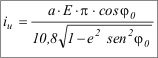
Por tanto, las fórmulas anteriores, expresadas en función del valor de la longitud de 1’ de paralelo de referencia i_u, quedarán de la forma:

       

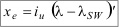
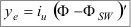
CÁLCULO DE LAS DIMENSIONES DE LA CARTA

Con lo visto hasta ahora, es posible calcular las dimensiones, horizontal y vertical, del esqueleto o marco de la carta sin más que calcular la diferencia entre las abcisas de los marcos E y W, considerando las esquinas SE y SW para la horizontal, y la diferencia entre las ordenadas de los marcos N y S, considerando las esquinas NW y SW para la vertical:

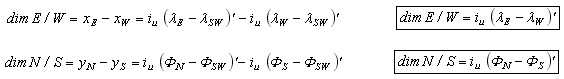
Ejemplo

Calcular las dimensiones horizontal y vertical de  un  esqueleto  cuyos  marcos  son: Marco N = 35º 19’ N, Marco S = 35º 10’ N, Marco W = 03º 24’ W y Marco E = 03º 10’ W; la escala de la carta será de 1:20.000, y el paralelo de referencia el de 35º 14’ 30” N. El elipsoide empleado como  referencia  será  el  Internacional  con a = 6.378.388 m y f = 1/297.

Como primer paso se determinará el valor de la excentricidad e y e²:

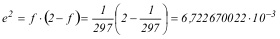
y, por tanto:

A continuación, se determinará el valor de la longitud de 1’ del arco de paralelo de referencia, con la fórmula ya estudiada anteriormente:

Para el cálculo de la dimensión horizontal del esqueleto se empleará la expresión correspondiente:

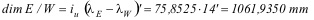
Para el cálculo de la dimensión vertical será necesario calcular primero las latitudes aumentadas F_N y F_S, correspondientes a las latitudes f_N y f_S de los marcos N y S. Para ello, se empleará la segunda igualdad de las expresiones analíticas de la proyección Mercator (la que hace referencia al cálculo de las y; para más información véase el artículo sobre el cálculo de coordenadas en Mercator), a la que se le añade el factor 10.800/p para dar F en minutos:

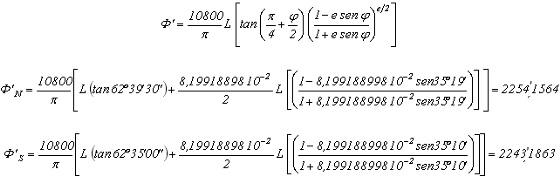
Del cálculo anterior se puede deducir la diferencia, en minutos, entre las latitudes aumentadas del marco Norte y del marco Sur, con lo cual ya se puede aplicar la fórmula correspondiente para el cálculo de la dimensión vertical:

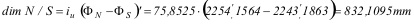
De los valores de las dimensiones horizontal y vertical, se deduce que la carta del ejemplo es horizontal.

CÁLCULO DE LA DISTRIBUCIÓN DE MERIDIANOS Y PARALELOS

Para este cálculo, será necesario disponer previamente del dato de intervalo D_mp, entre meridianos y paralelos, dado normalmente en minutos, y que generalmente será el mismo para ambos tipos de línea. Para el primer meridiano o paralelo, contados a partir de la esquina SW del esqueleto, se elegirá una cifra en longitud y latitud que de números enteros. Como se puede dar el caso de que la latitud o longitud de los marcos del esqueleto no sean números enteros, la distancia entre los marcos del esqueleto y la primera línea de meridiano o paralelo, puede ser distinta a la que determina el intervalo que establece el resto de la distribución de líneas. Cuando se llegue al borde contrario del marco de la carta, tanto en longitud como en latitud, es decir, a la esquina NE, podrá volver a ocurrir lo mismo.

Previo al cálculo de la distribución de líneas, se habrá efectuado el de la determinación de las dimensiones de la carta, por lo que la longitud i_u será un dato conocido y calculado con la expresión correspondiente que ya hemos visto antes. Este valor i_u multiplicará al intervalo D_mp, en minutos, elegido para representar las líneas. Este intervalo es constante para establecer la separación entre meridianos, excepto para el caso mencionado de que los marcos no sean cifras enteras. Una vez elegida la cifra entera correspondiente al primer meridiano, y calculada su distancia al origen, bastará con ir sumando a ella el producto  i_u× D_mp para determinar la posición de cada meridiano de acuerdo al intervalo D_mp elegido.

Sin embargo, para el caso de los paralelos, será necesario calcular una a una, las latitudes aumentadas F,correspondientes a cada uno de los paralelos definidos de acuerdo al intervalo elegido. Para ello, se empleará la segunda igualdad de las expresiones analíticas de la proyección Mercator (que también hemos citado antes), a la que como se ha dicho se le añade el factor 10.800/p para dar las latitudes aumentadas buscadas en minutos. Entonces, se calcularán las diferencias existentes, en minutos, entre las latitudes aumentadas F correspondientes a cada paralelo y la latitud aumentada F_SW del marco S. Una vez obtenidas todas las diferencias, se multiplicarán, cada una de ellas, por el valor i_u. El resultado será la distancia vertical, en milímetros, que separa cada paralelo del origen SW.

Ejemplo

Siguiendo con el mismo caso que en el ejemplo para la determinación de las dimensiones de la carta, se pide determinar la distribución de líneas si el intervalo entre ellas es de D_mp= 1’.

En este caso, los marcos E y W del esqueleto, son cifras enteras de minutos, por lo que se sumará, directamente a los marcos, el producto:

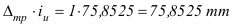
Así, considerando como origen de coordenadas la esquina SW, se empezará sumando, a la longitud del Marco W = 03º 24’W, la cantidad de 75,8525 mm para determinar los meridianos cada D_mp= 1’, hasta llegar al  Marco E = 03º 10’ W. De esta forma se obtendrán los datos del siguiente cuadro, en el que se puede observar que la última distancia es igual a la dimensión horizontal calculada para el esqueleto:

Para determinar la distribución de los paralelos, se necesita calcular primero, las latitudes aumentadas para cada una de las latitudes que establecen los intervalos. Para ello, volvemos a utilizar la segunda igualdad de las expresiones analíticas de la proyección Mercator, a la que como hemos dicho se le añade el factor 10.800/p para dar las latitudes aumentadas en minutos. Las latitudes aumentadas F_N y F_S, de los marcos N y S, ya se han hallado al calcular las dimensiones del esqueleto, así que se continuará calculando la latitud aumentada del siguiente paralelo, el 35º 11’ N, y posteriormente, las siguientes con el intervalo D_mp= 1’ hasta llegar al Marco N = 35º 19’ N. Así, se obtiene:

Aplicando sucesivamente, se llegará a obtener la siguiente tabla en la que se puede observar que la última distancia es igual a la dimensión vertical calculada para el esqueleto, con lo cual completamos el ejercicio: