CÁLCULO DE COORDENADAS Y PARALELO DE REFERENCIA EN LA PROYECCIÓN DE MERCATOR
José Manuel Millán Gamboa, Instituto Hidrográfico de la Marina
Jefe Producción de Cartografía Electrónica (ENC), (2004) Instituto Hidrográfico de la Marina.
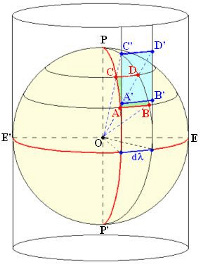
Fig.1
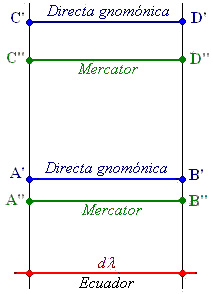
Fig.2
Las cartas que se utilizan para la navegación, tanto marítima como aérea, cumplen la condición de ser conformes, es decir, conservan los ángulos en cualquier dirección. Así, las líneas que marcan la dirección, entre dos puntos de la representación, son rectas. Esto es especialmente útil para la navegación ya que las derrotas y demoras, se corresponden con líneas rectas, lo que facilita su trazado, el mantenimiento del rumbo, y la medida de distancias entre dos puntos cualesquiera.
Mercator fue el primer cartógrafo que diseñó una proyección de este tipo, que es la que actualmente lleva su nombre. Para su desarrollo partió de una proyección no conforme como es la cilíndrica gnomónica directa (proyección efectuada, desde el centro de la Tierra, sobre un cilindro tangente al Ecuador. Fig. 1). Mediante esta proyección los puntos A, B, C y D, sobre la esfera, se convertirán en los puntos A', B', C' y D' proyectados sobre el cilindro. Así, el paralelo AB se convertirá en el A'B' y el CD en el C'D'. Esta proyección no es conforme por no ser iguales: a) la relación entre la longitud del pararlelo de la esfera y la longitud del proyectado, y b) la relación entre la longitud del meridiano sobre la esfera y la del meridiano proyectado. Para conseguir, a partir de esta proyección, otra que tuviera la propiedad de la conformidad, tuvo la idea de manipular la relación b) para hacerla igual a la a) y, para ello, calculó en qué cantidad debería alterar la distancia entre paralelos y Ecuador de esa proyección, es decir, buscó unas nuevas posiciones A"B" y C"D" (Fig.2) delos paralelos proyectados A'B' y C'D'. Con esta modificación consiguió que las deformaciones de la proyección en la dirección de la latitud fuesen iguales a las existentes en la dirección de la longitud y, como consecuencia, la conservación de los ángulos, y por tanto, la conformidad buscada. Como resultado del cálculo necesario para conseguirlo, obtuvo que la separación final entre paralelo y Ecuador debía ser igual a la existente entre ellos sobre la superficie de la Tierra pero multiplicada por el factor:
![]() (1)
(1)
Para llegar a esta conclusión, y las consideraciones que siguen a continuación, se tomó, y se tomará, como superficie de referencia de la Tierra, la del elipsoide de revolución, de manera que las formulas que se exponen sean de aplicación directa para cualquier datum geodésico de referencia que se adopte. Así, en el factor (1), a es el semieje mayor del elipsoide, que se toma como referencia para la figura de la Tierra, y N, la gran normal en el punto de latitud f, que define el paralelo en cuestión, y que se calcula según las siguientes expresiones en las que e es el valor de la primera excentricidad del elipsoide y f es el aplanamiento del elipsoide. :
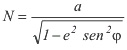 (2) donde: e2 = (2 f - f2) (3)
(2) donde: e2 = (2 f - f2) (3)
Siguiendo con el desarrollo de Mercator, teniendo en cuenta (1) y efectuando la integral correspondiente para pasar de elementos diferenciales a distancias concretas sobre la Tierra, se deduce que en el plano de representación de la Mercator, las distancias que separan cada paralelo del Ecuador son menores que las correspondientes de la proyección cilíndrica gnomónica directa, tal como se muestra en la Fig.2, en la que se puede observar como, los segmentos A''B'' y C''D'', se encuentran más próximos al Ecuador que sus correspondientes A'B' y C'D'. El resultado de ese desarrollo da las expresiones analíticas de la proyección Mercator que son:
 (4)
(4)
El parámetro F de la segunda ecuación se denomina latitud aumentada o latitud creciente. De acuerdo a estas fórmulas, se puede afirmar que el sistema de referencia ortogonal OXY (Fig.4), del plano de representación, tendrá su origen en el punto de cruce del meridiano de Greenwich con el Ecuador, ya que para x = 0 e y = 0 , han de ser f= 0 y l= 0 (Fig.3). Además, para f= 0 siempre será y = 0 , por lo que el eje X coincide con la transformada del Ecuador. Para l= 0 siempre será x = 0 , por lo que el eje Y coincide con la transformada del meridiano de Greenwich.
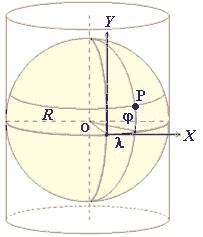
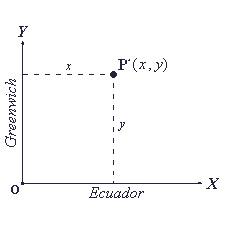
Fig. 3 Fig.4
Las expresiones (4) verifican las condiciones de contorno que Mercator estableció para la proyección que hoy lleva su nombre:
- La transformada del Ecuador es una línea recta a lo largo de la cual se conservan las distancias.
- Las transformadas de los meridianos son líneas rectas, paralelas y equidistantes entre ellas, normales a la transformada del Ecuador.
- Las transformadas de los paralelos son líneas rectas, paralelas a la transformada del Ecuador, es decir, normales a las transformadas de los meridianos.
- La proyección es conforme.
Ejemplo
Para calcular las coordenadas Mercator en un punto cualquiera como puede ser, por ejemplo, uno central en la península Ibérica, de f = 40º 30' N y l = 003º 30' W , sobre un elipsoide WGS84 en el que a = 6.378.137 m y f = 1/298.257223563 , se hará:
y, por tanto:
sustituyendo los valores obtenidos en (4):
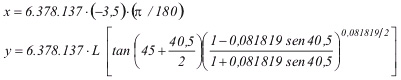
![]()
Las coordenadas así obtenidas se medirán, en la carta mercatoriana, desde el cruce de las transformadas del meridiano de Greenwich y del Ecuador, según el sistema ortogonal cartesiano OXY de la figura anterior.
EL PARALELO DE REFERENCIA
Cuando se ha de realizar la representación de una zona concreta alejada del Ecuador, como podría ser, por ejemplo, una carta que cubriera las aguas próximas a la península Ibérica, los marcos de la representación se elegirán de tal forma que abarquen solamente esas aguas, descartando representar otras zonas más alejadas. Así, resulta que en el área cartografiada no aparecerá la línea automecoica de representación, que sirve como medida de escala verdadera, y que de acuerdo a las condiciones de contorno establecidas para la proyección de Mercator, es la línea del Ecuador. Fuera de esta línea automecoica, el concepto general de escala es irreal ya que, en una misma representación, no existe un valor fijo para ella en todos los puntos, sino que la escala varía, en general, de un punto a otro. En el caso de la proyección Mercator este efecto se ve acentuado en casos como el expuesto para la península Ibérica, demasiado alejada del Ecuador.
Para evitar este inconveniente, y reducir estas variaciones de escala, se recurre al artificio de la reducción de las coordenadas mediante un factor de reducción de escala que no altera la conformidad ni la naturaleza de la representación, pero que afecta a todos los elementos lineales y superficiales, de forma que actúa como un factor multiplicador de la escala original E que provoca que la escala real E', en un punto cualquiera de la representación presente menores variaciones. Este artificio, consiste en variar la primera de las cuatro condiciones de contorno establecidas, en el sentido de que la línea recta a lo largo de la cual deben conservarse las distancias, sea la transformada de un paralelo que pase por la zona a representar, en lugar de la transformada del Ecuador. Al paralelo así elegido se le denomina paralelo de referencia, y su latitud se suele representar por f0. Para materializar este artificio, bastará con efectuar la proyección sobre un cilindro secante a la esfera en ese paralelo f0, en lugar de utilizar un cilindro tangente en el Ecuador.
Si la zona a representar se encuentra en las proximidades de un punto A como el de la Fig.5, se utilizará un paralelo de referencia f0, que puede ser aquel cuya latitud es la del punto A. El cilindro secante, por tanto, lo será justo en esa latitud, de forma que su intersección será exactamente el círculo del paralelo de A. Considérese el elipsoide inscrito en él. Si el elipsoide terrestre original tenía un semieje mayor a , este nuevo elipsoide tendrá un semieje mayor a', que tendrá por valor:
a' = N cos f0 (5)
El elipsoide así definido, es un sistema de elipsoide y cilindro tangente que posee las mismas propiedades con las que se ha definido la proyección de Mercator, y por tanto, es igual de válido para representar cualquier zona del elipsoide original. La única diferencia existente, es el valor del semieje mayor antes y después de considerar el cilindro secante. Esta diferencia vendrá determinada por la relación matemática entre ellos, comportándose como un factor de escala que indica que la proyección se realiza en un modelo de similares propiedades, pero de distinto tamaño. Así, las fórmulas de correspondencia (4), adaptadas para el caso del elipsoide inscritos al cilindro secante, siendo N el valor de la gran normal en A, tendrán la forma:
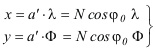 (6)
(6)
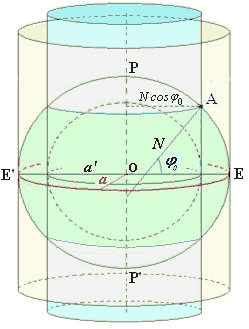
Fig. 5
Para estas fórmulas (6), el origen de abcisas será el meridiano de Greenwich y el origen de ordenadas será el Ecuador, pero en ambos casos, establecidos sobre el elipsoide inscrito. Es decir, las coordenadas x e y así obtenidas, estarán medidas sobre modelos distintos a los del elipsoide original, por lo cual sólo serán comparables a través del mencionado factor de escala que los relaciona:
![]() (7)
(7)
Ejemplo:
Calcular las coordenadas Mercator para el lugar del ejemplo anterior de f = 40º 30' N y l = 003º 30' W , utilizando un paralelo de referencia en la latitud de f0 = 35º 14' 30” N sobre un elipsoide WGS84 en el que a = 6.378.137 m y f = 1/298.257223563 .
Como primer paso se determinará el valor de la excentricidad e de acuerdo a (3) y de la misma forma que en el ejemplo anterior:
A continuación, con (2) se calculará el valor de la gran normal N para la latitud del paralelo de referencia:
![]()
Con estos valores, y las formulas de correspondencia (6), se obtendrán las coordenadas buscadas:
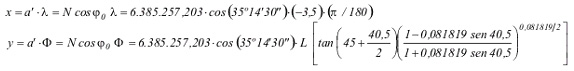
x = 318.566,36 m
y = 4.015.508,95 m
Como puede observase, para el mismo punto del ejemplo anterior, al utilizar el paralelo de referencia, se obtienen unas coordenadas distintas con valores absolutos de x e y menores. Es debido a la reducción de escala producida por el empleo del paralelo de referencia, que tiene el significado intuitivo de estar utilizando un modelo de proyección de distintas dimensiones. Este efecto tiene su importancia a la hora de representar, en Sistemas de Información Geográfica (SIG), información náutica procedente de cartografía náutica que emplean distintos paralelos de referencia, lo cual es frecuente. Las coordenadas de los elementos geográficos contenidos en cartas con distintos paralelos de referencia, no son comparables, por proceder de modelos distintos. Por tanto, para su correcta representación en un SIG y efectuar comparación en solapes, etc., previamente se debe deshacer este efecto, transformando las coordenadas al modelo original de cilindro tangente en el Ecuador en cada una de las cartas empleadas. Para ello, bastará con dividir las coordenadas obtenidas en este ejemplo por el factor de escala (7), obteniéndose así las del ejemplo anterior.